DSA Tutorial: Master Merge Sort Algorithm
What is Merge Sort?
Merge Sort is one of the most elegant and efficient Divide and Conquer algorithms in Data Structures and Algorithms (DSA). It works by dividing an unsorted array into smaller parts, sorting them individually, and then merging them back together in sorted order.
This approach makes Merge Sort fast, stable, and predictable, making it a go-to choice for large datasets where performance matters.
⚙️ How Merge Sort Works
Merge Sort operates in two main phases:
- Divide Phase:
- The array is recursively divided into two halves until each sub-array contains only one element.
- A single-element array is inherently sorted.
- Conquer (Merge) Phase:
- The sub-arrays are then merged back together in order.
- At each merge step, elements are compared, and the smaller one is placed first, ensuring the result is sorted.
This recursive “split and merge” process continues until the full array is reconstructed — completely sorted!
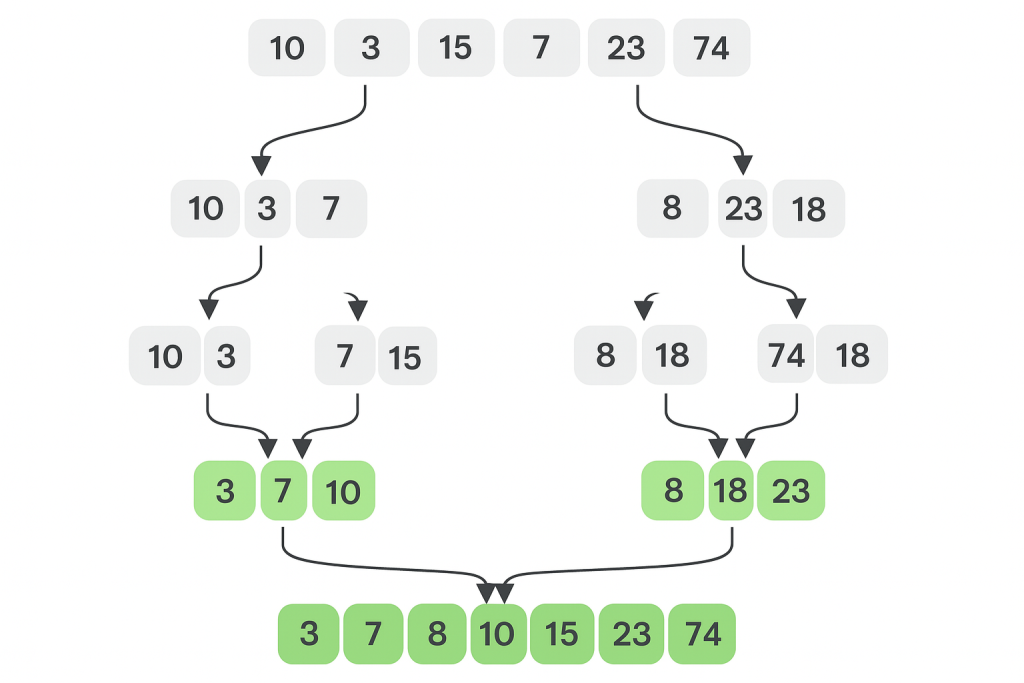
Initial Array
[10, 3, 15, 7, 8, 23, 74, 18]
Step 1: Split into halves
- Left:
[10, 3, 15, 7] - Right:
[8, 23, 74, 18]
Step 2: Split again
- Left →
[10, 3]and[15, 7] - Right →
[8, 23]and[74, 18]
Step 3: Sort pairs
[10, 3]→[3, 10][15, 7]→[7, 15][8, 23]→[8, 23](already sorted)[74, 18]→[18, 74]
Step 4: Merge sorted pairs
[3, 10]+[7, 15]→[3, 7, 10, 15][8, 23]+[18, 74]→[8, 18, 23, 74]
Step 5: Final merge
[3, 7, 10, 15]+[8, 18, 23, 74]→[3, 7, 8, 10, 15, 18, 23, 74]
[3, 7, 8, 10, 15, 18, 23, 74]
🔍 Step-by-Step Example
Let’s say we have an array:[12, 8, 9, 3, 11, 5, 4]
Step 1: Split the array repeatedly
→ [12, 8, 9] and [3, 11, 5, 4]
→ [12] [8, 9] [3, 11] [5, 4]
Step 2: Merge the smaller arrays
→ [8, 9, 12] and [3, 4, 5, 11]
Step 3: Final merge
→ [3, 4, 5, 8, 9, 11, 12]
Your array is now sorted — simple and efficient!
💡 Key Highlights
- Algorithm Type: Divide and Conquer
- Sorting Nature: Stable (retains relative order of equal elements)
- Best Use Case: When dealing with large datasets and linked lists
- Recursive or Iterative: Can be implemented both ways
🧩 Merge Sort in Action (Python Example)
def mergeSort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = mergeSort(arr[:mid])
right = mergeSort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
unsortedArr = [12, 8, 9, 3, 11, 5, 4]
print("Sorted array:", mergeSort(unsortedArr))
🧮 Merge Sort Time Complexity
| Case | Time Complexity | Explanation |
|---|---|---|
| Best Case | O(n log n) | Even when already sorted, merge steps are required |
| Average Case | O(n log n) | Balanced recursive division and merging |
| Worst Case | O(n log n) | Consistent performance across all cases |
| Space Complexity | O(n) | Requires extra space for merging |
🧠 Why Learn Merge Sort?
- Foundation for understanding Divide and Conquer strategy
- Commonly used in interview questions
- Provides insight into recursive problem-solving
- Forms the base for advanced sorting algorithms
🧭 Visualize Merge Sort
Watch how Merge Sort splits and merges an array dynamically through our interactive animation tool on GoNimbus!
👉 Experiment, visualize, and understand recursion in real-time.
🚀 Ready to Master DSA?
Explore our next tutorials:
- Quick Sort – Learn another powerful divide-and-conquer algorithm
- Heap Sort – Understand sorting with priority queues
- Radix Sort – Non-comparative sorting made simple
Start your journey toward mastering Data Structures and Algorithms with GoNimbus — your guide to coding clarity.